Talboten efektua (I): fenomeno bitxi baten jaiotza

Daniel Eceizabarrena

Gizakiari guztiz naturala zaion elementua da argia, eta hark inguraturik bizi izan da beti. Hala ere, askotan espero ez diren fenomeno miresgarriak uzten dizkio argiak begien bistan. Honen adibide ezin hobea dugu aztertzera goazen Talboten efektua.

Gure protagonista nagusia Talboten alfonbra izenez ezagutzen da eta bera dugu Talboten efektuaren adierazpenik deigarriena. Datozen lerroetan irudi polit hau sortzearen arrazoiak azaltzen saiatuko gara, baina egoki deritzogu lehenago Talbot zientzialaria aurkezteri. Izan ere, bera izan zen lehenbizikoz fenomenoa behatu zuena, baina ez da ziurrenik merezi bezain ospetsua, nahiz eta fenomenoari izena ematen dion.

William Henry Fox Talbot

Erresuma Batuko hegoaldean jaioa, William Henry Fox Talbot (Dorset, 1800 – Wiltshire, 1877) harrigarria den diziplina anitzetan aritutako zientzialaria izan zen. The Royal Society erakundearen kide izendatu zuten 1831n matematikan egindako lan garrantzitsuengatik. Ekarpen azpimarragarriak egin zituen kimikan, elektrizitatean eta astronomian ere. Natur-zientziez gain, etimologian eta arkeologian ere aditua zen; hori erakusten du, behintzat, gaur egun Iraken dagoen Asiriako Ninive hiriko zenbait inskripzio kuneiforme itzuli izanak. Hori guztia gutxi balitz, politikan aritzeko denbora ere izan zuen, Londresko Parlamentuan aulkia lortu baitzuen 1832an. Edonola ere, esan liteke kalotipoa dela bere ekarpen handiena, gaur egun ezagutzen ditugun argazkien aitzindarietan garrantzitsuenetarikoa baita.

Italiako Comoko lakuaren ertzeko paisaia eskuz marrazten saiatzen ari zen 1833ko oporraldian, eta nonbait marrazkigilea baino zientzialari hobea zen Talbot, lan hori egingo zuen makina sortzea bururatu baitzitzaion. Bururatu ez ezik, 1839an argiarekiko sentikorra zen papera sortu eta haren gainean irudiak islatzeko metodoa garatu zuen. Garai bertsuan Parisen arrakasta itzela izan zuen Dagerrotipo famatuarekiko abantaila zuen, gainera. Hura ez bezala, irudi negatibo bat sortzeko gai zen, eta nahi bezainbeste kopia positibo sortzeko erabil zitekeen. Frantsesaren asmakuntzak, ordea, hedapen handiagoa izan zuen, seguruenik Talbotek bere ideia patentatu zuelako.

Kalotipoaren sortze prozesu honetan optika-ikerketak egin behar izan zituen Talbotek halabeharrez. Egoera horretan gertatu zen Talboten efektuaren aurkikuntza, izan ere, 1836an argitaratu baitzuen horri buruzko artikulua. Modu kualitatiboan eta xehetasun handirik gabe deskribatu bazuen ere (ziurrenik garaiko muga teknikoengatik), argi dago fenomeno honen lehen erregistroa dela. Guk ere bide kualitatibo horixe egingo dugu, baina zehaztasun handiagoa ematen saiatuko gara.

Esperimentuaren planteamendua

Talboten efektua fenomeno optiko mikroskopiko bat da, hots, eskala txikian gertatzen den argiaren fenomeno bat, eta argia sareta batean zehar iraganaraztearen ondorioz sortzen da. Efektua ikusteko, sareta alde batetik argiztatu eta argiak sareta zeharkatu ostean, beste aldean zer ikusten den behatu behar dugu.

Nahiz eta kontzeptualki oso esperimentu sinplea izan, aberastasun ikaragarria dauka egitura aldetik, eta ez da batere erraza argiak sareta zeharkatu ondoren duen portaeraren analisia egitea.

Hasteko sinplifikazio batzuk ontzat emango ditugu. Sareko ebaki guztien artean tarte berdina dagoela onartuko dugu, eta tarte horrekin alderatuz ebakien zabalera oso txikia dela. Gainera, egoera bi dimentsiotan aztertuko dugu hirutan egin beharrean. Zehatzago, saretoaren norabide bertikala ez dugu kontuan hartuko, saretako ebakiak bertikalak direnez egoera berdina izango baita altuera guztietan. Ondorioz, ebaki bertikalak dituen sareta tarte berdinez aldenduta dauden hutsuneak dituen marra zuzen bihurtuko da, eta argia perpendikularki etorriko zaio.

Hasieratik problema zuzenean ebatzi beharrean, lehenik zulo bakar batekin eta bi zulorekin zer gertatzen den ikusiko dugu. Horretarako, ezinbestekoa da uhinen fisikan berebiziko garrantzia duten hiru kontzeptu jorratzea: uhinen difrakzioa, Huygensen printzipioa eta Youngen bi zirrikituen esperimentua.

Difrakzioa eta Huygensen printzipioa

Demagun saretak zulo bakarra duela, 5. irudiko egoeran gaudelarik. Saretaren norabide perpendikularrean datorren argi-uhina zulo bakar horretatik igaroko da beraz, eta gure helburua saretaren beste aldetik zer ikusiko dugun jakitea da.

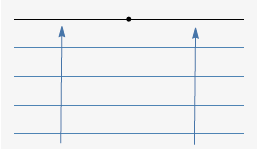
Goiko hau azaltzen du, beste gauza askoren artean, Huygensen printzipioak. Izan ere, 1690ean argitaratutako Traité de la lumière liburuan, Christiaan Huygens holandarrak (Haga, 1629 – Haga, 1695) argiaren propagazioaren printzipio nagusia deskribatu zuen: argiaren iturria puntu bakar bat denean, uhin esferikoen bidez hedatzen da.

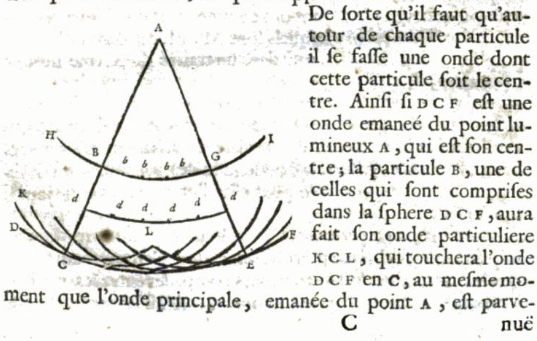
Gatozen gure saretaren egoerara. Argi-uhinak sareta jotzean zuloa duen puntuan bakarrik zeharkatuko du. Huygensen printzipioari jarraituz, puntu horrek uhin esferikoa sortuko du. Fenomeno hau da difrakzio izenez ezagutzen denaren oinarrizko adibidea da.

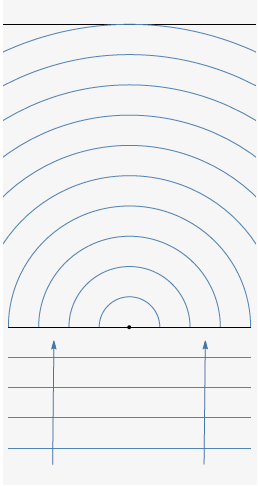
Jakin nahi dugu irudian beltzez markatutako pantailan zer ikusiko dugun. Argi dago saretako zuloaren parean argiaren intentsitatea handia izango dela, zuzen zuzenean iristen baita uhina bertara. Hala ere, geroz eta zuloaren paretik gehiago urrundu, orduan eta intentsitate txikiagoa izango du iristen den argiak, distantzia gehiago egin behar izan duelako jatorritik.

Huygensen printzipioari esker, beraz, argi geratu zaigu zer gertatzen den zirrikitu bakarreko saretan. Hurrengoan, bi zirrikitu dituen sareta aztertuko dugu, ondoren Talboten esperimentuko egoera ondo ulertu ahal izateko. Ikusi berri dugunaren antzeko zerbait behatuko al dugu? Erantzuna, hurrengo atalean.

Erreferentzia bibliografikoak

• Huygens, Christiaan, (1690). Traitée de la lumière. Leiden: Pieter van der Aa.
• Talbot, Henry Fox, (1836). LXXVI. Facts relating to optical science. No. IV. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 9 (56), 401-407, DOI: 10.1080/14786443608649032
• Malcolm, Daniel, (2004). William Henry Fox Talbot (1800–1877) and the Invention of Photography. In Heilbrunn Timeline of Art History. The Metropolitan Museum of Art, New York.
• Complete Dictionary of Scientific Biography, Encyclopedia.com: “Talbot, William Henry Fox“. (Kontsulta data: 2018ko azaroaren 2a)

Egileaz: Daniel Eceizabarrena matematikaria da eta Basque Center for Applied Mathematics (BCAM) ikerketa-zentroko ikertzailea.