Dozena erdi ariketa 2019ko udarako (4): Posizioaren bila
Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko astelehenero ariketa matematiko bat izango duzu, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure laugarren ariketa: Posizioaren bila.
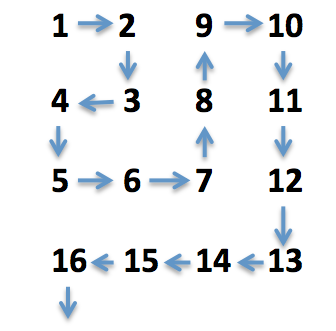
4) Zenbaki arruntak irudiak erakusten duen moduan antolatu ditugu. Zein zutabetan eta errenkadatan egongo da 2019 zenbakia? (Zutabeak ezkerretik eskuinera eta errenkadak goitik behera hartuko ditugu.)
Ariketak “Calendrier Mathématique 2019. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
2 iruzkinak
Beno, aste honetakoak buruhauste gutxiago eman dizkidala uste dut.
16ko blokeak ditugunez, 2019/16 eginez 126,1875 lortzen dugu. Hau da, 126 bloke oso ditugu eta bloke berriaren barruan zein posiziotan doan ikusi behar da. Asike 2019 – 126*16 = 3. 3a 2. lerroa eta 2. zutabean dagoenez, eta 126 bloke 504 lerro direnez, 2019 506. lerroan eta 2. zutabean egongo da
Arratsalde on;
Niri honako hau ateratzen zait; 7 garren errenkada eta 45 garren zutabea.
Nik modu honetan enfokatu dut;
01—02—09—10
04—03—08—11
05—06—07—12
16—15—14—13
… eta abar;
diagonalean dauden zenbakiak sekuentzia bat jarraitzen dute;
(01)01=01+00
(02)03=01+02
(03)07=03+04
(04)13=07+06
honela atera dezakegu azaltzen ez diren gainontzeko diagonalen baloreak;
(05)21=13+08
(06)31=21+10
Parentesi artean zutabe eta errenkadeen kopurua (hauxe da 31 zenbakia 6×6=36 elementu dituen diagonal batetan egongo da).
Excel horrialde bat erabilita atera dut;
(45) garren diagonalaren balorea 1981 izango dela (45×45=2025) berez lauki honen barruan dago gure zenbakia. ¿Non ordea?
Ikusten ba dugu 1,2,3,4, Sekuentzian zenbakiak ordularien horratzen sentidu berdina jarraitzen dute, urrengoan (5,6,7,8,9) kontrakoa. Gure kasuan (45) baita ere ordularien kontrako sentidua jarraituko dute, hauxe da ezkerretik eskubira 1981 balorea duen zutaberaino (45 garren zutabea eta 45 garren errenkada) eta handik gora, niri ateratzen zait honako hau;
7 garren errenkada eta 45 garren zutabea.