Zenbaki ospetsurik bada matematikan, hori pi da, letra (greko) baten izena duen zenbakia. Aurreko artikulu batean Pi eguna aipatu genuen, martxoaren 14a, alegia, π = 3.14 izateagatik aukeratua. Baina 3.14 ez da π-ren balio zehatza, haren adierazpen hamartarreko lehen zifra dezimal biak hartuta lortzen den zenbakia da, ez besterik. Idatz daiteke garapen hamartar osoa?
Duela bi mende eta erdi Johann H. Lambert-ek frogatu zuen π irrazionala dela. Horren ondorioz, garapen hamartarrak infinitu zifra dezimal ditu eta, gainera, ez dago bloke bat behin eta berriro errepikatzen dena (periodoa), bestela zenbaki arrazionala izango bailitzateke. Hortaz, garapeneko zifra pilo bat idatzita ere, beti daude gehiago eta, gainera, ezin dugu aurresan zein izango den jarraipena. Garapeneko dezimalak kalkulatzeko, formula on bat eta denbora edo/eta tresna egoki bat behar dira. Duela urtebete, 50 bilioi (5 x 1013) zifra dezimal kalkulatzeraino heldu ziren. Zer esanik ez, teknologiaren aurrerapen izugarriaren eskutik etorri da halako lorpena. Ikus dezagun π-ren dezimalen kalkuluaren bi mila urte eta gehiagoko bilakaera hori.

Arkimedesen bidea
Zirkunferentziaren luzeraren eta diametroaren arteko erlazioa da π. Ikuspegi geometriko hori zen nagusi Antzinatean eta ez zuten erlazioa berez zenbaki gisa ikusten. Geometrian oinarritu zuen Arkimedesek proportzio horren bilaketa (π-ren balioarena guretzat) K.a. III. mendean. Ia bi mila urtez erabili zen Arkimedesen metodoa π-ren hurbilketak lortzeko.
Hasteko, zirkunferentzia baten barruan eta kanpoan hexagono erregularrak kokatu zituen, zirkunferentzian inskribatutako eta zirkunskribatutako poligonoak, alegia. Zirkunferentziaren luzera hexagono horien perimetroen artean dago. Gero, alde-kopurua bikoiztuz, dodekagonoak kokatu zituen. Barruko poligonoaren luzera handitu eta kanpokoarena txikitu egiten zen horrela, eta π tarte estuago batean kokatu. Behin eta berriro alde-kopurua bikoiztuz, geroz eta hurbilketa hobea lortzen da. Arkimedesek berak 96 aldeko poligonoraino eraman zituen kalkuluak; horrela, 3 10/71 eta 3 1/7 artean kokatu zuen π-ren balioa. Idazkera hamartarrera pasatuz, 3.140845… < π < 3.142857… dugu, eta hor ikusten da π = 3.14 diogunean zifra dezimal biak zuzenak direla.
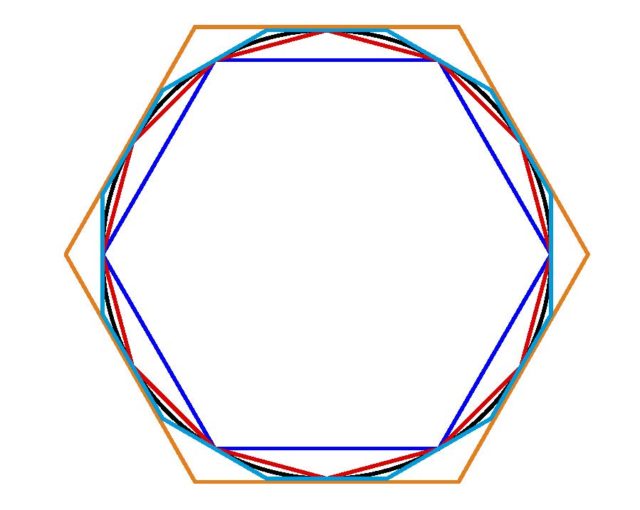
Hurrengo mendeetan etekina atera zioten Arkimedesen metodoari alde gehiago kontuan hartuz. Ptolomeok II. mendean 377/120 balioa eman zuen eta horrek hiru dezimal zuzen ditu. Gero, Asian aurkitzen ditugu ekarpenik aipagarrienak, zientziaren arrastoa ia desagertuta egon baitzen mendebaldean denbora luzean. Bereziki Txinako emaitza batzuk nabarmentzen dira: Liu Huiren algoritmoa (III. mendea) eta Zu Chongzhiren hurbilketa (V. mendea). Azken honek 3.1415926 eta 3.1415927 artean kokatu zuen π.
Arkimedesen poligonoen metodoa erabiliz azken emaitza garrantzitsua Ludolph van Ceulen alemaniarrak eman zuen XVII. mendearen hasieran: 35 zifra dezimal lortu zituen, 262 aldeko poligonoen bidez, urte askoko lanaren ondoren. Holandan izan zen irakasle eta Leidenen hil zen. Kalkulaturiko π-ren balioa Leidengo hilobian ipini zioten (3. irudia). Denbora luzez Alemanian Ludolphsche Zahl (Ludolphen zenbakia) esan zioten π-ri.

Kalkuluaren aroa
Kalkulu infinitesimala XVII. mendean sortu zen eta aro berri bat ekarri zuen matematikara. Handik aurrera funtzioen garapen infinituak ohiko egin ziren eta π-ren balio hurbilduak lortzeko ere baliatu ziren. Horren adibide,
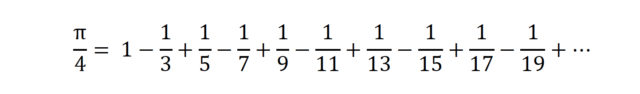
formula daukagu. Puntuek adierazten dute infinituraino jarraitu beharko genukeela gaiak jartzen berdintza gertatzeko. Berez, batura partzialen limitea hartu behar da eta, horregatik, nahi beste hurbildu gaitezke ezkerreko baliora behar adina gai hartuta eskuinean. Guregana Gottfried W. Leibniz (1676) eta James Gregory (1671) izenei lotuta heldu den formula da, baina Sangamagrama-ko Madhava astronomo indiarrak jada ezagutzen zuen haiek baino 250 urte lehenago. Formula bera ez da oso erabilgarria praktikan, gai gehiegi behar direlako zehaztasun egoki bat lortzeko. Baina hobetu daiteke, eta Madhavak berak antzeko serie hobe bat erabiliz, 11 dezimal lortu zituen π-rako.
Goiko formula hori, berez, arku tangente funtzioaren seriezko garapenaren kasu bat da. Oro har,
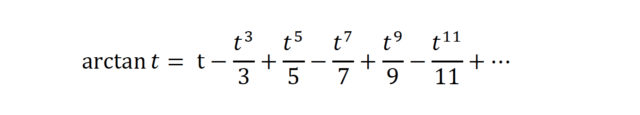
dugu eta t = 1 eginez gero, Madhavaren formula lortzen da, arctan 1 = π/4 baita. (arctan t = x izateak esan nahi du x radianeko neurria duen angeluaren tangente trigonometrikoak t balio duela.) Serieak arinago konbergitzen du t txikiago izanda eta, horregatik, beste formula batzuk baliatuz, hala nola,
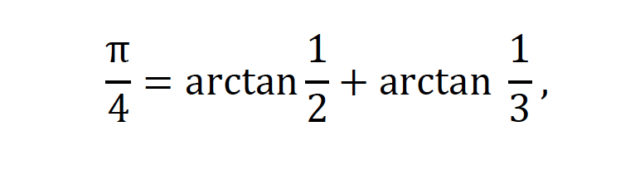
beste garapen hau lortuko genuke:
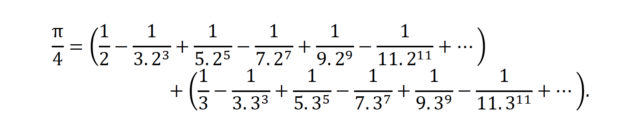
Lehengoak ez bezala, honek arin ematen ditu zifra dezimal zehatzak. Eskuineko atalean idatzi ditugun apur horiek batuta 3.14156158… lortzen da, lau zifra dezimal zehatz, alegia.
Hortik aurrera, π-ren dezimal ezagunen zerrenda asko hazi zen. Bereziki aipagarria da John Machin ingelesaren ekarpena,
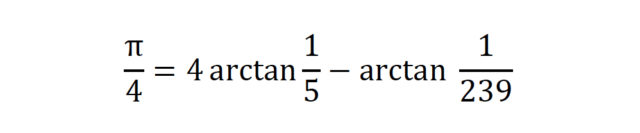
formula lortu ondoren, 100 zifra dezimal kalkulatu baitzituen 1706an. Ez zen hor gelditu kalkulua eta aro horretako ekarpenik luzeena William Shanks ingelesak eman zuen 1873an: Machinen algoritmoa erabiliz eta urte asko kalkuluari emanda, 707 dezimal plazaratu zituen. Handik 70 urtera, mahai gaineko kalkulagailu batekin lanean, konturatu ziren bakarrik lehenengo 527ak zirela zuzenak. Horregatik aldatu behar izan zituzten goiko 1. irudian agertzen direnak.
Ordenagailuen aroa
Ordenagailuak kalkuluak arinago egiteko sortu ziren eta horrek erabat aldatu zituen π-ren dezimalak lortzeko aukerak. Lehen ordenagailua, ENIAC ospetsua, 1949an jarri zuten eginkizun horretan, eta 70 orduko lanaren ondoren π-ren 2037 dezimal kalkulatu zituen. Handik aurrera, eten gabe egin du gora dezimal-kopuruak, besteak beste, makinen ahalmenari formula hobeak elkartu zaizkiolako.
Hurrengo taula honek laburbiltzen du azken 70 urteetako bilakaera:
| Urtea | Makina | Denbora | Dezimal-kopurua |
| 1958 | IBM 704 | 1.7 ordu | 10 000 |
| 1961 | IBM 7090 | 8.7 ordu | 100 265 |
| 1967 | CDC 6600 | 28 ordu | 500 000 |
| 1973 | CDC 7600 | 23.3 ordu | 1 001 250 |
| 1987 | NEC SX-2 | 36 ordu | 134 217 700 |
| 1989 | IBM 3090 | 1 011 196 691 | |
| 1997 | HITACHI SR2201 | 91 ordu | 51 539 600 000 |
| 1999 | HITACHI SR8000 | 83.5 ordu | 206 158 430 000 |
| 2002 | HITACHI SR8000 | 600 ordu | 1 241 100 000 000 |
| 2011 | etxekoa | 371 egun | 10 000 000 000 050 |
| 2020 | etxekoa | 303 egun | 50 000 000 000 000 |
Uneko errekorraren jabe den Timothy Mullican-ek azaltzen duenez, piezak erosita muntatu zuen ordenagailua (ikus 4. irudia) eta, behin kalkulurako programa prestatuta, 303 egun mantendu zuen makina lanean, 2020ko urtarrilaren 29an gelditu arte, orduan lortu baitzuen 50 bilioigarren tokiko dezimala.

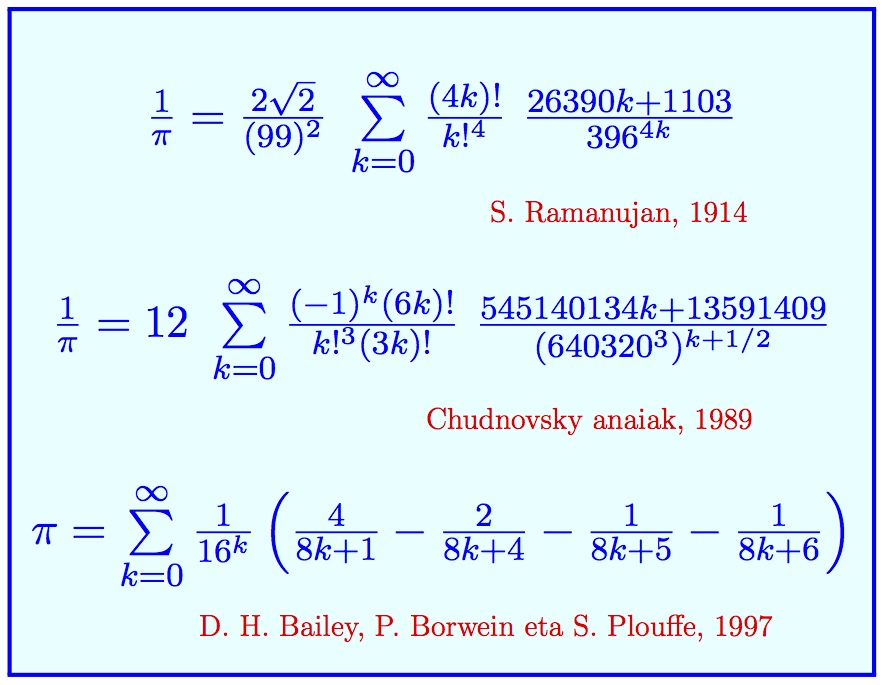
Ordenagailuen gaitasunaz gain, formula berriak aipatu behar dira. Ramanujan matematikari indiar harrigarriak formula sinestezinak aurkitu zituen π-rako, hala nola 5. irudian agertzen den lehen hori. Formula zaharrak baino arinago ematen ditu π-ren dezimalak, eta geroago beste aldaera batzuk asmatu dira. Chudnosky anaiek emandako aldaera batekin (hori ere 5. irudian) mila milioi dezimal lortu zituzten 1989an. Azken aldiko errekor batzuetan algoritmo bera erabili dute, batugai bakoitzak 14 dezimal zuzen gehitzen dituelako. Bestalde, 5. irudian agertzen den hirugarren formulak (BBP deitzen zaio, egileen abizenak hartuta) badu berezitasun bat: 16 oinarriko sisteman, eta ondorioz sistema bitarrean ere, toki zehatz bateko dezimala kalkula daiteke, aurrekoak ezagutu barik.
Eta hori guztia, zertarako?
Zertarako balio du π zenbakiaren hainbeste zifra dezimal ezagutzeak? Egia esateko, ezertarako ere ez… Benetan π-ren balioa mundu errealean erabiltzen denean, kalkulurik zorrotzenetan ere, duela 500 urte ezagutzen zen zehaztasuna nahikoa eta sobera da. Orduan, zerk pizten du batzuen interes hori? XVIII. mendera arte pentsa zitekeen garapen hamartarra amaitu egingo zela edo periodiko bihurtu, hots, π zenbaki arrazionala izango zela. Norbaitek esperantza hori bazuen, Lamberten emaitzak zapuztu zion: π irrazionala da.
Garai modernoetan, ordenagailua kalkuluetan sartu zutenean, makinaren gaitasuna probatzeko balio dezakeela esan ohi dute. Hala zioen Timothy Mullicanek, esaterako, orain arteko errekorra lortu zuenean. Dena dela, beste errekor batzuen antzera, badirudi honek ere ez duela pizten Guinness World of Records ospetsuan agertzetik aparteko interesik.
Gehiago jakiteko edo ikusmiran ibiltzeko
- π-ren hurbilketaren historia eta haren kronologia.
- Timothy Mullicanen bloga: gaur egungo errekorra ezarri zuen lana azaltzen du.
- Milioi bat dezimal orrialde bakar batean: https://www.piday.org/million/.
- π kalkulatzeko erabili diren formulak eta algoritmoak aurkezten dituen Jesús Guilleraren artikulu bat.
- π-ren zenbat zifra dezimal gogoratzen dituzu? Horretan ere bada lehia bat, ea nork gehiago esan. Orain arte buruz zifra dezimal gehien esan duena Suresh Kumar Sharma indiarra da: 2015ean 70 030 eman zituen, 17 ordu eta 14 minutuan. Harrigarria! Hori guztia eta gehiago, Pi World Ranking List webgunean.
- Pifilologia deitzen da π-ren zifra dezimalak gogoratzeko baliabide mnemoteknikoen alorra.
- Azken hamarkadako errekorrak egiteko y-cruncher programa erabili dute. Alexander J. Yee da programaren sortzailea eta beste konstante matematiko ezagun batzuk kalkulatzeko ere erabili dute. Programaren webgunean informazio guztia duzue.
- Zure jaioteguna edo nahi duzun data aurkituko dizu π-ren zifra dezimalen artean Find Your Pi Day webguneak.
Egileaz:
Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da UPV/EHUn.
1 iruzkina
[…] Piramidearen oinarri poligonalak badu matematikekin harremana. Matematikak baditu figura famadunak, denok ezagutzen ditugun horiek. Beraien artean dugu zenbaki irrazional bitxi bat: “pi“. Pi zirkunferentzia baten luzeraren eta haren diametroaren arteko erlazioa (zatidura) bera da edozein delarik horretarako erabiltzen dugun […]