Aurtengo seigarren ariketarako ez dugu erantzunik jaso. Beste guztietan erantzun zuzenak heldu dira, baita okerren bat ere. Bosgarren ariketari Andonik eman dion erantzuna kenduta, besteetan inork ez digu azaldu zein izan den emaitzara heltzeko bidea.

Mikelek eta @amorroik erantzun zuzen bana lortu zuten. Hona erantzun osoa:
Zenbakia abcd bada,
(1000a+100b+10c+d)+(a+b+c+d)=2017
eskatzen ari gara. Bistan da a=1 eta b=9, edo a=2 eta b=0 beharrezkoak direla.
- a=1 eta b=9 hartuta, 1001+909+11c+2d=2017 dugu, hau da, 11c+2d=107. Honek c=9 eta d=4 soluzioa ematen du, hots, 1994.
- a=2 eta b=0 hartuta, 2002+11c+2d=2017 dugu, hau da, 11c+2d=15. Hemendik, c=1 eta d=2 ateratzen da, hots, 2012.
Zifren batura kenduz gero, ez dago soluziorik
(1000a+100b+10c+d)-(a+b+c+d)=2017
behar dugu orain. Hori lortzeko, a=2 eta b=0 beharko dugu. Orduan, 1998+2c=2017 lortu behar da, eta hori ezinezkoa da.

Lau erantzun zuzen izan ditu ariketak: Amorroik, Andonik, Manexek eta Koldok emandakoak.
Lehen jaurtialdi biek 1-2 eta 3-8 edo 1-8 eta 3-2 aukerak bakarrik uzten dituzte. Hirugarrenak erakusten du 3-2 ezinezkoa dela. Beraz, 1-2 eta 3-8 fitxak ditugu. Era berean, 5-6 eta 4-7 dira beste fitxak. Baturarik handiena 2+6+7+8=23 da.

Erantzun zuzenaz gain, aholkua ere eskaini zion Koldok Anartzi.
Seigarren partidatik bederatzigarrenera 17 puntukoa da Anartzen batezbestekoa. Lehen bost partidetakoa 17 baino txikiagoa izan behar denez, gehienez 84 puntu egin ditu Anartzek bost partida horietan denetara. Hamar partidatan 180 puntu egin dituenez, azken partidan gutxienez 28 puntu sartu ditu.
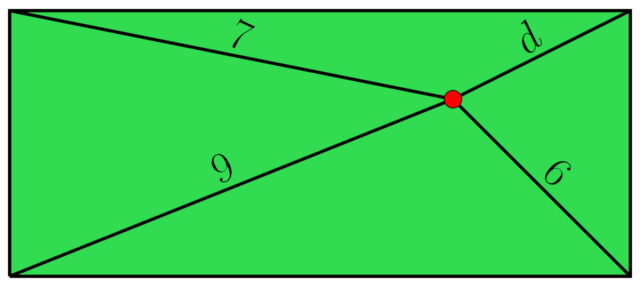
Honetan ere fin ibili zen Koldo. Hona azalpena:
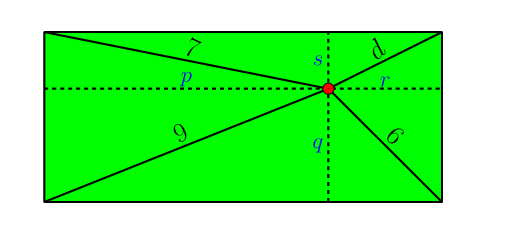
Pitagorasen teorema erabiliz,
?² + ?² = 7² , ?² + ?² = 9² , ?² + ?² = 6², ?² + ?² = ?²
Lehenengoaren eta hirugarrenaren baturari bigarrena kenduz gero,
?² + ?² = 7² + 6² − 9² = 4
lortzen da. Beraz, d=2 da.

Jarraitutako bidea azaldu zigun Andonik emaitza zuzenarekin batera. Koldok ere zuzen.
Azken kilometroa egiteko t segundu eman baditu, azken aurrekoa t+5 segundutan egin du, hamahirugarrena t+10 segundutan, eta horrela. Lehenengoa egiteko t+70 segundu behar izan ditu. Orduan,
? + (? + 5) +( ? + 10) + ⋯+ (? + 70) = 51×60 = 3060
Hemendik, 15t+525=3060, eta t=169 segundu. Azken kilometroa 2 minutu eta 49 segundutan egin du.
Andoniren ebazpidea desberdina da, oso dotorea.
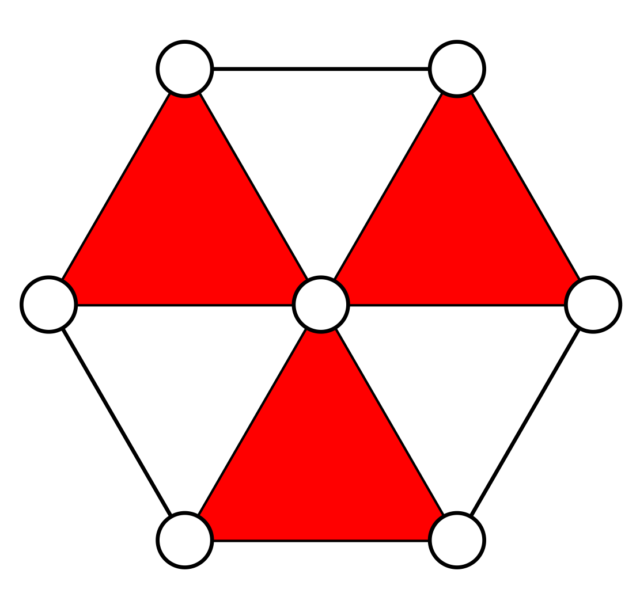
Erantzunik izan ez duen ariketa bakarra da hau, hona emaitza eta azalpena:
Kanpoko zenbakien batura 3ren multiploa izango da, eta 1etik 7rainoko zenbakien batura 28 da. Beraz, erdiko zenbakia 1, 4 edo 7 da ezinbestean.
Demagun erdikoa 1 dela. Kanpoan 2-7, 3‐6 eta 4-5 bikoteak joango dira. 2 zenbakia kokatzeko sei aukera daude. Horietako bakoitzak 7 zenbakia finkatzen du. 3 zenbakia kokatzeko lau aukera geratzen dira eta horiek 6 zenbakia finkatzen digute. Azkenik, 4 zenbakia kokatzeko bi aukera ditugu eta horiek 5 zenbakia finkatzen dute. Denetara, 1 erdian egonda 6×4×2 = 48 modutan jar daitezke zenbakiak.
Era berean, 4 edo 7 ipiniz gero, 48 modu ditugu eskatutako baldintza betetzeko. Hortaz, 3×48 = 144 modutan jar daitezke zenbakiak eskatutako baldintza betetzeko.
Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.