Erantzunak zuzen daude. Koldotxuren azalpena da politena. Jokalari bakoitzak lau partida jokatu ditu, beraz, ariketak ematen dituen kopuru guztiak batuz jokalari guztien adinen batura lau bider agertuko da. Hortaz, 660:4=165 da adin guztien batura. Gazteenak, 165 – 142 = 23 urte ditu.
Hemen ere erantzunak zuzenak dira: 28 eta 39. Zifra biko zenbakiak banan-banan probatuz egin daiteke, baina ez da oso bide dotorea. Iñakik eta Joseluk erantzun polita eman digute. Zenbakiaren zifrak a (hamarrekoak) eta b (unitateak) izanda, 10a + b – ab = 12 eskatzen ari gara. Hortik aurrera arrazoibide desberdinak daude:
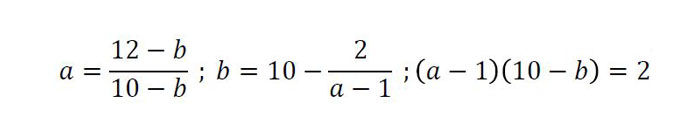
adierazpen baliokideak agertzen dira hartu ditugun erantzunetan. Horietako edozeinekin ikusten da a=2, b=8, eta a=3, b=9, direla soluzio posible bakarrak.
Iñakiren erantzuna zuzena da. Karratuaren diagonala 4√2 da. Dei dezagun r zirkunferentzia txikiaren erradioa. Orduan, hurrengo irudian agertzen den notazioarekin, AM = 4, MP = r eta PC = r√2 dira.
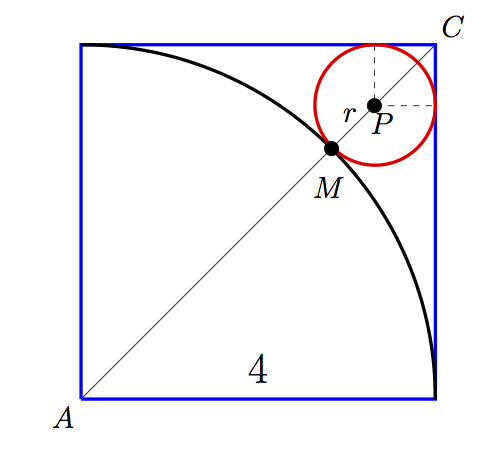
Beraz, 4√2=4+r (1+√2) ekuazioa lortzen dugu, eta
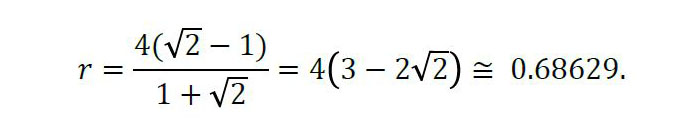
Iñakik sekuentzia bat aurkitu du diagonalean dauden zenbakietarako, Excelen laguntzaz, eta horrekin kokatu du 2019 dagokion lekuan.
Horren ordez, beste bide hau errazagoa izan daiteke. Zutabe bakoitien goiko aldean karratuak daude (1, 9, 25…) eta errenkada bikoitien ezkerreko zenbakia ere karratua da (4, 16, 36…). Zein da 2019ren gainetik hurbilen dagoen karratua? 2019= 45² – 6 da eta 45. zutabearen goiko zenbakia 45² = 2025 denez, sei errenkada beherago aurkituko dugu 2019. Ariketaren erantzuna, beraz, 45. zutabea eta 7. errenkada da.
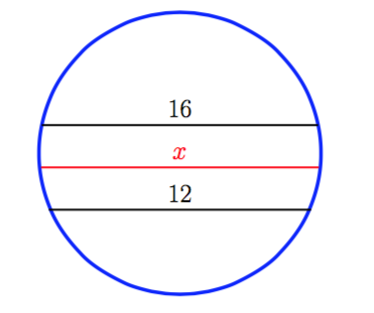
Iñakik bidali duen azken erantzuna zuzen dago. Idatz ditzagun R zirkunferentziaren erradioa, d1 zentrotik korda handira dagoen distantzia eta d2 korda txikirainokoa. Pitagorasen teorema erabiliz,
R2 = 82 + d12 eta R2 = 62 + d22 .
Bigarren ekuaziotik lehenengoa kenduta, d22 – d12 = 28 dugu, edo
(d2 – d1)(d2 + d1) = 28.
Korden arteko distantzia 7 dela esan digute. Kordak zentrotik alde banatan badaude, d2 + d1 = 7 eta, orduan, d2 – d1 = 4. Alde berean badaude, d2 – d1 = 7 eta d2 + d1 = 4 izango lirateke, baina hori ezinezkoa da. Beraz, d1 = 1.5 eta d2 = 5.5 dira. Korda bietatik distantzia berera dagoena, zentrotik 2 cm-tara egongo da. Beraz, l izanik bilatzen ari garen luzera,
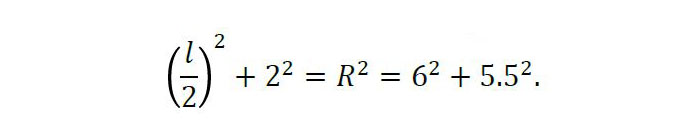
Kalkuluak eginez, l = 2√62.25 = √249 ≅ 15.7797 cm.
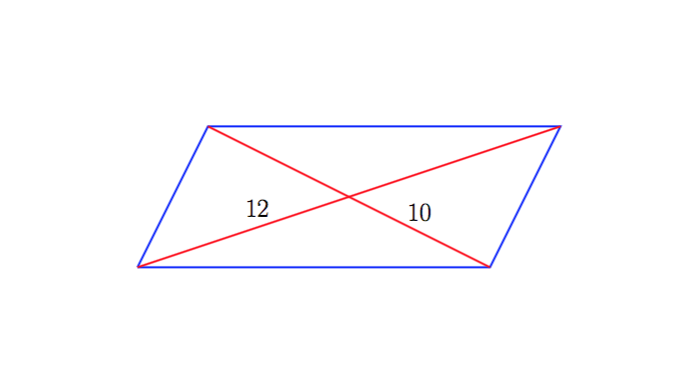
Heldu diren erantzun biak ondo bideratuta daude, baina azkenean biak okertu egin dira. Hurrengo irudiak erakusten duen notazioa erabiliko dugu.
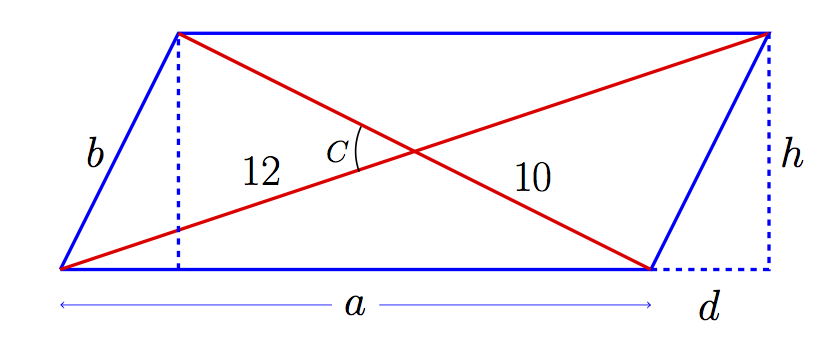
Lehen bidea (Iñakirena, baina angeluak sartu barik). Pitagorasen teorema eta azalerarako eman diguten informazioa erabiliz, ekuazio hauek ditugu:
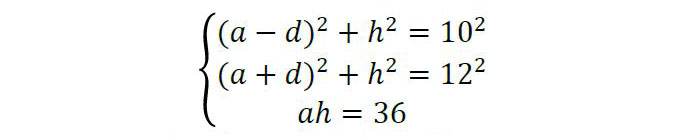
Hirugarren ekuazioak h=36/a ematen digu. Bigarren ekuazioari lehenengoa kenduta, 4ad = 4, , edo ad = 11 dugu. Hortaz, d = 11/a. Lehenengo ekuazioan ordezkatuz,
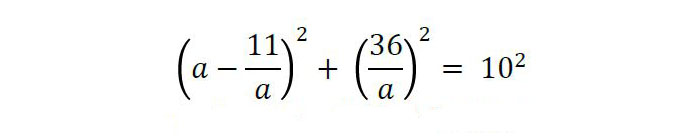
ekuazioa lortzen dugu, edo a4 – 122a2 + 1417 = 0. Bigarren mailako ekuazioa dugu a2 ezezagunerako, eta a2 = 109 eta a2 = 13 soluzioak ditu. Hortaz, a = √109 edo a = √13 izan daiteke. Beste aldea lortzeko, b2 = d2 + h2 egingo dugu. Horrek b = √13 ematen du, a = √109 bada, eta a eta b-ren balioak trukatuta beste kasuan. Horrela, √109 ≅ 10.44 eta √13 ≅ 3.61 dira aldeen luzerak.
Bigarren bidea (Koldotxurena). Paralelogramo baten azalera kalkulatzeko formula hau dugu:
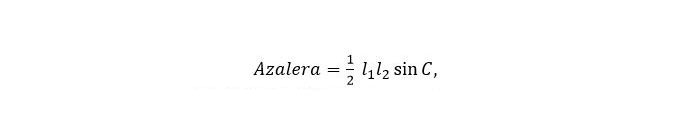
non l1 eta l2 diagonalen luzerak diren eta C diagonalen arteko angelua. (Ez nuen formula hau gogoan. Eskerrik asko, Koldotxu.) Ariketak emandako datuak ordezkatuz, sinC = 3/5 lortzen da. Aldeak kalkulatzeko diagonalen erdiek eta alde bakoitzak osatzen duten triangeluan kosinuaren teorema erabiliko dugu:
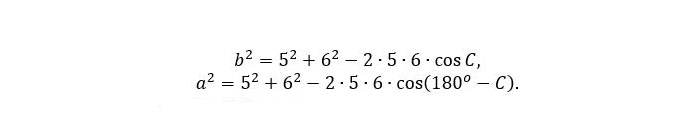
C angeluaren sinua ezagutzen dugunez, kosinua kalkulatzeko ez dugu angeluaren balioa behar, (sinC)2 + (cosC)2 = 1 baita. Orduan, cosC = 4/5 eta cos(180o – C)= -4/5. Hortik, a2 = 109 eta b2 = 13.
Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.
3 iruzkinak
Eskerrik asko, Javi, azalpenengatik eta ariketak jartzeagatik! Datorren urtean, hobeto 😉
Milla esker azalpenengatik, eta ea hurrengo batean “pleno” egiten dugun.
Proposatutako problemak oso interesgarriak izan dira, nire klaseetan erabiltzeko modukoak. Mila esker eta hurrengo arte.