Dozena erdi ariketa 2020ko udarako: erantzunak

Javier Duoandikoetxea

1. Niko eta Aneren artean 80 euro dituzte. Nikok Aneri honek duen beste diru eman dio. Ondoren, Anek Nikori galdetu dio ea zenbat diru duen eta beste horrenbeste eman dio. Gero, Nikok berriro eman dio Aneri honek duen beste diru eta ezer barik gelditu da. Zenbat diru zuen Nikok hasieran?Erantzun zuzenak heldu dira eta ondo azalduta. Bide aljebraikoa, aldagaiak erabiliz, edo atzekoz aurrera, aljebra erabili barik; bietara ikusi dugu erantzuna.

Hasieran Nikok x euro eta Anek y euro badituzte, hauek dira urratsak:

Niko	Ane
x	y
x-y	2y
2x-2y	2y-(x-y)=3y-x
2x-2y-(3y-x)=3x-5y	6y-2x

Amaieran Nikok 0 euro eta Anek 80 euro dituztenez, urrats bakoitzean nork bikoizten duen kontuan hartuta, atzekoz aurrerako taula hau bete dezakegu:

Niko	Ane
0	80
40	40
20	60
50	30

Hortaz, hasieran Nikok 50 euro zituen eta Anek, 30.

2. Karta batzuetan idatzita daude bi zifrako lehen bederatzi zenbaki lehenak (11 da txikiena eta 41 da handiena). Kartak ordenatu nahi ditugu erregela hau betez: elkarren alboan dauden karten zenbakien aldea 2-ren berretura da. Zenbat modutan egin dezakegu?

Erantzun zuzen bat hartu dugu: lau modutan egin daiteke. Badirudi baten batek ez zuela galdera ulertu, zenbaki lehen terminoa zer zen ez zekielako. Argi dezagun, hasteko, euskarazko zenbaki lehen hori número primo (es) edo nombre premier (fr) dela.

Bi zifrako lehen bederatzi zenbaki lehenak hauek dira: 11, 13, 17, 19, 23, 29, 31, 37 eta 41. Eta ordenatzeko agindua da elkarren alboan dauden zenbaki biren arteko aldea 2, 4, 8 edo 16 izatea. Eskema honek erakusten du zein joan daitekeen zeinen alboan:

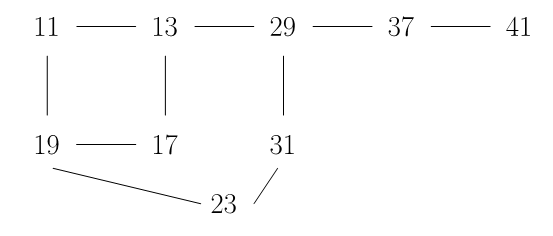
Bistan da 41 mutur batean egongo dela. Jar dezagun hasieran. Derrigorrean, 41-37-29 izango dugu, eta hurrengoa 13 edo 31 izango da. Erraz ikusten da 13-rekin jarraituz gero, ezin direla denak hartu. Beraz, 41-37-29-31-23-19 lortuko dugu. Hortik amaitzeko aukera bi ditugu, 17-13-11 edo 11-13-17. Gainera, zerrenda biak atzekoz aurrera hartuta, beste bi lortzen dira. Hauek dira soluzioak:

3. ABC triangelua zuzena da (A-n du angelu zuzena). AB = 3 m eta AC = 4 m dira. DE eta BC paraleloak dira eta 1 m da bien arteko distantzia. Zein da ADE triangeluaren azalera?

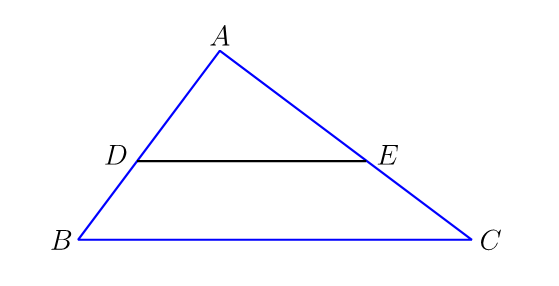
Triangeluak antzekoak dira (angeluak berdinak, aldeak proportzionalak). Luzeren arteko erlazioa aurkitu behar dugu.

Triangelu handiaren katetoak 3 eta 4 direnez, hipotenusa 5 izango da. Azalera (3×4)/2 = 6 m² da. Hortaz, hipotenusari dagokion altuera (A erpinetik beheraino), 2.4 m da. DE-tik oinarrira 1 m dagoenez, triangelu txikiaren altuera 1.4 m izango da. Beraz, luzeren arteko proportzioa 1.4/2.4 edo 7/12 izango da. Triangelu txikiaren aldeak 3×7/12, 4×7/12 eta 5×7/12 izango dira. Eskatutako azalera 49/24 m² da. Iñakiren erantzuna zuzena da, beraz.

4. 39-ren zatitzaileak 1, 3, 13 eta 39 dira. Zatitzaileen azken zifrak 1, 3 eta 9 dira. Zein da zatitzaileen azken zifretan 0-tik 9-rainoko guztiak dituen zenbakirik txikiena?

Zatitzaile baten amaierako zifra 0 bada, zenbakiarena ere bai. Hortaz, 10-en multiplo bat behar dugu. Beste zatitzaile baten azken zifra 9 bada, zatitzaile hori 9, 19, 29… izango da.

Demagun 9 dela zatitzailea; orduan, 90-en multiplo bat bilatzen dugu. 90-en zatitzaileak 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45 eta 90 dira. Bakarrik 4 eta 7 amaierak falta dira. Baldin 90 x 2 = 180 hartzen badugu, 4 amaiera lortzen dugu, baina ez 7. Baina 90 x 3 = 270 hartuz gero, orduan bai ditugu amaiera guztiak, 27 eta 54 zatitzaileak direlako.

Zergatik da 270 txikiena? 19 zatitzailea bada, 190-en multiploak beharko genituzke. 190 berak ez du baldintza betetzen eta gainerakoak 270 baino handiagoak dira. 29 edo handiagoa bada 9 amaiera duen zatitzailea, edozein aukera 270 baino handiagoa da.

Koldotxuk erantzun zuzena utzi digu. Bidalitako beste erantzunak, 2520, ariketaren baldintza orokorra betetzen du, baina ez da lor daitekeen txikiena.

5. Zirkulu baten erradioa √2 da. Zati bat jan diogu, zentrotik pasatzen den 1 erradioko zirkulu bat gainezarriz. Zenbat da zirkulu handiari gelditzen zaion azalera?

Zirkulu handiaren azalera 2π da eta txikiarena, π.

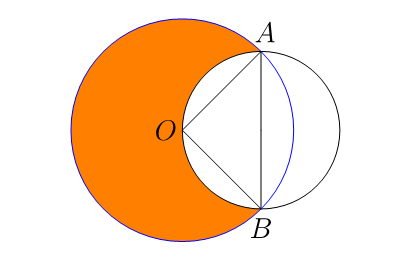
Irudiko OAB triangelua zuzena da, Pitagorasen teoremak erakusten duenez. Triangelu horren azalera 1 da.

AB zuzenkia zirkulu txikiaren diametroa denez, horren ezkerretara kendu dugun azalera, π/2 izango da. Eskuinetara kendu dugun azalera kalkulatzeko, zirkulu handiaren OAB sektoreari triangelua kendu beharko diogu. Sektorea zirkulu osoaren laurdena da, zentroan eratzen duen angelua zuzena delako. Beraz, sektorearen azalera 2π/4 = π/2 izango da, eta kendu duguna π/2-1.

Dena kontuan hartuta, zirkulu handiari gelditzen zaiona hau izango da:

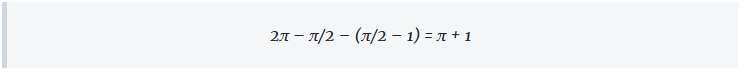
Galder Gonzalezek eman du erantzun zuzena ariketa honetan.

6. Zenbaki oso bati 52 kenduta eta 52 gehituta, bietan karratu perfektuak (zenbaki osoen karratuak) lortzen dira. Aurkitu propietate hori duten zenbaki guztiak.

Izan bedi N bilatzen dugun zenbakia. Hau dakigu:

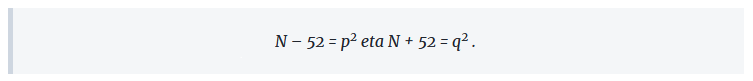
Hemen, p eta q zenbaki osoak dira. Ekuazioen kendura eginez, edo batean N askatuta bestean ordezkatuz, hau lortzen dugu:

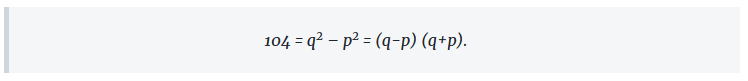
104 zenbaki oso biren biderkadura moduan honela idatz daiteke:

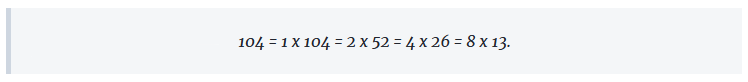
Hortik, aukera hauek ditugu:

• q + p = 104, q – p = 1;
• q + p = 52, q – p = 2;
• q + p = 26, q – p = 4;
• q + p = 13, q – p = 8.

Bakarrik bigarrenak eta hirugarrenak ematen dituzte balio osoak p eta q-rako, eta hauek dira:

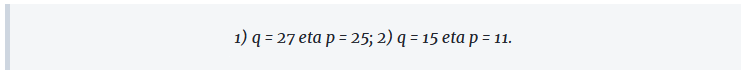
Horiekin, N = 677 eta N = 173 balioak ateratzen dira.

Iñakik eman du ariketa honen erantzun zuzena.

---

Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.